Login🔥
New to Challenges? Register➡️Are you a Replyer?
Access with Reply credentials
The ins and outs of a Reply Code Challenge solution
Introduction
The Reply Code Challenge is an online team-based programming challenge. It was first created in 2018 by a team of coding experts from Reply, called the Reply Code Masters. Based on their experiences, they decided to design a challenge powered by Reply for Replyers. This was then opened up to students and professionals.
Over four intense hours, participants from all over the world come together to solve algorithm-based optimisization problems. In 2020, the third edition of the Challenge involved more than 20,000 registered users.
The Code Challenge asks you to solve an optimisation problem. In other words, to find the best solution from a set of possible solutions.
Different input files are provided with each problem and you need to find the best solution to the input files by writing an algorithm using any language of your choice.
The cases proposed in the input files cannot be solved in an optimal way as, given their size, they would take too long to run with standard resolution techniques. So you’re asked to find the best possible solution to win the challenge.
In this article, the first of a series, we’ll lift the lid and show you a step-by-step approach to solving the problem posed at Reply Code Challenge 2020.
The problem
You can find the problem statements in the 2020 sandbox.
But here’s a brief explanation:
The aim of this problem is to assign Replyers, either Developers or Project Managers, to empty seats in the Reply office in the most efficient way. Thus, a map of the office will be provided with a list of Developers and a list of Project Managers. [...] While working, it's always good to have skilled colleagues nearby. So people with some common skills to complete the tasks, but also specific skills that they can share with, or learn from, other colleagues. Your task is to find the best place in the office for each Replyer, so that the work potential is maximized. You can decide not to assign a Developer or Project Manager, but this means missing the potential they would provide.”
We leave you to the problem statements for the details and we’ll makes some useful observations for later:
- A developer can't sit in a manager seat
- A project manager can sit, also, in a developer seat
- A project manager, for our purposes, is basically a developer without skills
- We can decide not to seat a person and, sometimes, we will be forced because there will be no seats available
- We can exchange a seated person for another, if it can increase the score
In the following sections we’ll use the term ‘developer’ to include developers and project managers, as it won’t affect the solution.
Solution structure
To code our solution, we’ll use C++. It’s the most suitable language for this kind of challenge as it has a lot of features, for example:
- faster and better performance compared to interpreted languages
- a wide standard library (the Standard Template Library) that provides a lot of optimised algorithms and data structures
- parallel applications that are easy and fast to write, using the standard thread library or any external library (as we’ll see later).
However, you’re free to use any language you want, but remember the above points are very important during a code challenge. So keep them in mind when training.
Whichever language you choose, we’ll use a top-down strategy to write our solution. This means thinking about the solution from a high point of view and breaking down (from top to bottom) complex functions into simpler ones that are easier to implement. The top-down strategy goes well with a team-base challenge as, once you’ve defined the interfaces for the top functions, it's easy to develop the solution in parallel by splitting tasks among teammates.
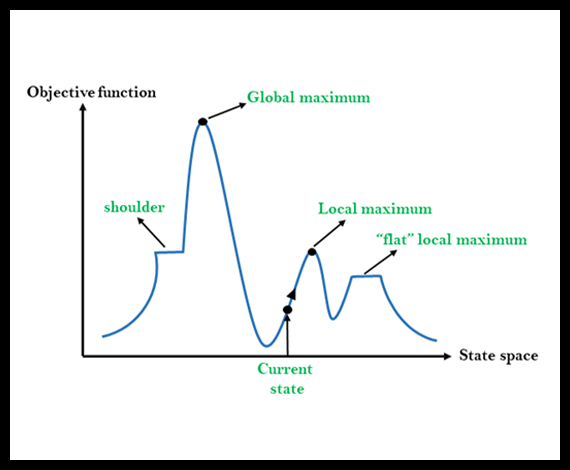
Finally, when it comes to writing code, we’ll write a greedy algorithm that optimises the solution with a hill-climbing technique.
A greedy algorithm is one that tries to solve a problem by making local optimal choices that approximate the best global solution. For us, the global problem is to assign developers to all the seats, while the local problem is to assign the best developer to a single seat.
As I mentioned, the size of the given input files mean solving the global problem is beyond our capabilities. Therefore, we’ll solve every single local problem separately by finding the developer that maximises the score for a given seat. So while solving all the local problems won't solve the global one, but as we’re facing an optimisation problem, the score will most likely be close to the optimal solution.
Hill climbing is a technique that, given a valid solution of the problem, attempts to find a better solution by making incremental changes to the solution.
For our problem, after assigning the developers to their seats we can freely swap a pair of developers if the swap increase the score. This way, we can always increase, not reduce the score (we’re climbing the hill of the score).
If we continue swapping developers to increases the score, we’ll eventually reach a maximum point (the top of our hill). In mathematical terms, we’ve reached a local maximum. The score of the local maximum depends only on the starting solution we chose.
In the following sections, we’ll explain and implement these functions, always with a top-down approach.
int main() {
cerr << "Reading the input..." << endl;
read_input();
cerr << "Finding the solution..." << endl;
find_solution();
cerr << "Score: " << get_score() << endl;
cerr << "Solution optimization..." << endl;
int step = 0;
while (optimize_solution())
cerr << "optimization step #"
<< ++step << " score: " << get_score() << endl;
cerr << "Write output" << endl;
write_output();
cerr << "Final score: " << get_score() << endl;
return 0;}
Initial setup:
libraries, input and output
In this section, we’re going to set up our C++ solution.
The first thing is to include all the libraries we need using the std namespace. Of course, the list of libraries depends on what we're going to write and can't be decided a priori. In a code challenge environment, we can add them gradually or include all the possible libraries, we can add them gradually or include all the possible libraries, even useless ones, just to speed up the writing of the solution – for example, using #include <bits/stdc++.h>.
#include <array>
#include <iostream>
#include <map>
#include <numeric>
#include <set>
#include <string>
#include <vector>
using namespace std;For the input data, we need to store the given grid and the information about developers and project managers. As I mentioned, we’re going to consider project managers as developers, so both their data will be saved in the same vectors.
// Input data
int W, H; // width and height of the map
int D; // numbers developers
int M; // number managers
vector<string> grid; // input map
vector<string> C; // developers company
vector<int> B; // developers bonus
vector<set<int>> S; // developers skillsFor the output data, we need to store the position for each developer in a vector. For convenience, we’ll use some other variables to help some operations – for example, a reverse look-up for the seated developers. I’ll explain their usefulness in the following sections.
// Solution data
vector<int> scores; // scores for each developer
// Output data
vector<vector<int>> assigned; // map place to developer
vector<array<int, 2>> pos; // developers position
// Constant for not-placed developers
const array<int, 2> NOT_PLACED = {-1, -1};Reading input data
After the initial definitions, the first step is to implement the read_input function to read the data from the given input files.
According to the problem statement, the input data are split into three types:
1. Grid data: the size of the grid and the chart matrix.
2. Developer data: the number of developers and, for each of them, the company, bonus and set of skills.
3. Project manager data: the number of project managers and, for each of them, the company and bonus.
As mentioned, we can consider project managers as developers so we’ll store both data in the same variables.
Another important thing to do to improve performance is to label each skill with an unique integer identifier. This way, we avoid a perform operation over strings, which are slower than the operation over integer numbers.
Implementation the read_input function will also allocate all the memory useful for analysing the output data.
Writing output data
In the output file, we have to print a line for each developer and each manager with their coordinates space-separated and, if we have not placed them, we have to put in an ‘X’.
Assuming to already have a valid solution in the pos array, the implementation of the write_output function is:
Reading the input data
//Read and parse input from file
void read_input() {
// Grid Data
cin >> W >> H; // Read office width and height
grid = vector<string>(H);
assigned = vector<vector<int>>(H, vector<int>(W, -1));
for (int i = 0; i < H; i++)
cin >> grid[i]; // Read map
// Developers data
cin >> D; // Read developers
// Allocate developers infos
C = vector<string>(D);
B = vector<int>(D);
S = vector<set<int>>(D);
// map skills to integer identifier
int scount = 1; // skill counter
map<string, int> skill_ids; // skills to integer mapping
// Read developers company, bonus and skills
for (int i = 0; i < D; i++) {
int ls;
cin >> C[i] >> B[i] >> ls;
for (int j = 0; j < ls; j++) {
string s;
cin >> s;
if (skill_ids[s] == 0) // not mapped skills
skill_ids[s] = scount++; // assigned an index
S[i].insert(skill_ids[s]);
}
}
// Managers data
cin >> M; // Read managers
// Reallocate vectors for managers
C.resize(D + M);
B.resize(D + M);
S.resize(D + M);
scores.resize(D + M); // scores for future use
// Read managers information
for (int i = 0; i < M; i++)
cin >> C[D + i] >> B[D + i];
// Output data
// Mark all developers as not placed
pos = vector<array<int, 2>>(D + M, NOT_PLACED);
}
Writing the output data
//Write output to file
void write_output() {
for (int i = 0; i < D + M; i++) {
if (pos[i] == NOT_PLACED)
cout << "X" << endl;
else
cout << pos[i][0] << " " << pos[i][1] << endl;
}
}
Evaluating the score
The total score of a valid solution is the sum of the score of each adjacent pair of developers. An easy way to evaluate it is to total the score for each seated developer with all its neighbours, and then halve it as we consider each pair twice.
We’ll implement three functions:
- get_score: evaluates the total score of a valid solution
- seat_score: evaluates the score between a developer and all its neighbours
- dd_score: evaluates the score between two developers
The get_score function iterates over the seated developers and calls the seat_score function:
// Total score of current solution
int get_score() {
int total_score = 0;
for (int i = 0; i < D + M; i++)
if (pos[i] != NOT_PLACED)
total_score += seat_score(i, pos[i]);
return total_score / 2;
}For a developer placed in a seat, its total score is the sum of the score with its four neighbours (left, right, up and down).
We implement the function eat_score call four times (one for each neighbour) and the dd_score function and accumulate the results. As we’re working in a limited grid, we must consider the boundaries and check the neighbour coordinates do not fall outside the input grid.
// evaluate the score between a developer
// and all its neighbhood (left, right, up, down)
int seat_score(int idx, const array<int, 2> pos) {
int tscore = 0;
int w = pos[0], h = pos[1];
// evaluate the score between (h, w) - (h-1, w)
if (h > 1)
tscore += dd_score(idx, assigned[h - 1][w]);
// evaluate the score between (h, w) - (h, w-1)
if (w > 1)
tscore += dd_score(idx, assigned[h][w - 1]);
// evaluate the score between (h, w) - (h+1, w)
if (h < H - 1)
tscore += dd_score(idx, assigned[h + 1][w]);
// evaluate the score between (h, w) - (h, w+1)
if (w < W - 1)
tscore += dd_score(idx, assigned[h][w + 1]);
return tscore;
}
Finally, the dd_score function evaluates the real score between two developers based on the problem statement formula. The score is composed of two parts: the company bonus and the skill bonus.
The company bonus is the product of the bonus of the two developers. It’s applied only if the two developers belongs to the same company.
The skill bonus is the product of common skills and different skills of two developers, which represent the intersection and the symmetrical difference of the two sets of skills. We can compute these two values efficiently using the ‘set find’ operation.
// Evaluate score between developers a and b
int dd_score(int a, int b) {
// one of the developers is invalid
if (a == -1 || b == -1)
return 0;
int tscore = 0; // total score
// same company, award bonus
if (C[a] == C[b])
tscore += B[a] * B[b];
int sa = S[a].size(); // # Skill of a
int sb = S[b].size(); // # Skill of b
// Compute intersction and symmetric difference
int intersection_size = 0;
int symdiff_size = 0;
for (int x : S[a])
if (S[b].find(x) != S[b].end())
intersection_size++;
symdiff_size = sa + sb - 2 * intersection_size;
tscore += intersection_size * symdiff_size;
return tscore;
}Finding the solution
As we’re writing a greedy algorithm, the find_solution function makes the optimal choice locally by finding, for each available seat, the best developer to put in it.
The find_best function is the core of the solution as it decides which developer to place in a seat.
To do this, we have to compute the score for each free developer, by simulating the seat assignment and computing the score reusing the function seat_score. Then, we take the highest score achieved of all the possible developers, if any.
Before putting a developer in a seat, we have to check if the seat is free or occupied. If it’s free then we can assign it. If it’s occupied by another developer, we perform a seat swap but only if the score of the new developer is higher than the score of the actual developer.
Lastly, if we want to speed up the solution, we can parrallelise the loop that evaluates the score for each developer as all scores are independent from each other. The simplest way to do this is to use the OpenMP API and put ‘#pragma omp parallel for’ before the ‘for loop’.
Filling the map
// Analyze each cell one by one
// and try to allocate the best developers
void find_solution() {
for (int h = 0; h < H; h++)
for (int w = 0; w < W; w++)
if (grid[h][w] != '#') // if this is available
find_best(h, w);
}
Placing the best developer
// best developers to set in ([h, w])
void find_best(int h, int w) {
int idx = -1; // index of the best developer
int best_score = 0; // max score of developer
int start = 0; // Starting index for developers
int end = D + M; // Ending index for developers
if (grid[h][w] == 'M')
start = D; // Exclude developers if manager place
// evaluate the score for each of the developers
#pragma omp parallel for
for (int i = start; i < end; i++)
if (pos[i] == NOT_PLACED)
scores[i] = seat_score(i, {w, h});
else
scores[i] = -1;
// find the best developer
for (int i = start; i < end; i++) {
if (pos[i] != NOT_PLACED)
continue;
if (idx == -1 || scores[i] > best_score) {
best_score = scores[i];
idx = i;
}
}
// no free developer found, exit
if (idx == -1)
return;
if (assigned[h][w] != -1) {
// Place already assigned
// Swap only if score increase
if (seat_score(idx, {w, h}) > seat_score(assigned[h][w], {w, h})) {
pos[idx] = {w, h};
pos[assigned[h][w]] = NOT_PLACED;
assigned[h][w] = idx;
}
} else {
// Empty place, assign developer
assigned[h][w] = idx;
pos[idx] = {w, h};
}
}
with another free if the total score increases
//Continue optimization if score is improved
// by at least 100 points
bool optimize_solution() {
int score_before = get_score();
find_solution();
int score_after = get_score();
return score_after - score_before > 100;
}
The optimization
Based on our approach, optimising a solution is very simple as we can reuse the function find_solution. Remember, you can swap a developer already seated with another free developer if the total score increases, following the hill climbing technique.
The optimize_solution simply calculates the score before and after a call to the find_solution function to see if the score increases. To avoid numerous optimisation iterations, we can decide to stop the loop if the score increases slightly – for example, by looking at the increasing percentage or by fixing a score threshold.
Final results
Once we’ve finished writing and debugging our solution, we can run it with the proposed input files.
If we run only the base solution, without the optimisation part, the scores for the 6 output files are:
1. output a_solar.txt: 36 points
2. output b_dream.txt: 2,669,880 points
3. output c_soup.txt: 590,770 points
4. output d_maelstrom.txt: 7,556,383 points
5. output e_igloos.txt: 3,976,050 points
6. output f_glitch.txt: 8,125,084 points

If we also run the optimisation part, all the scores increase:
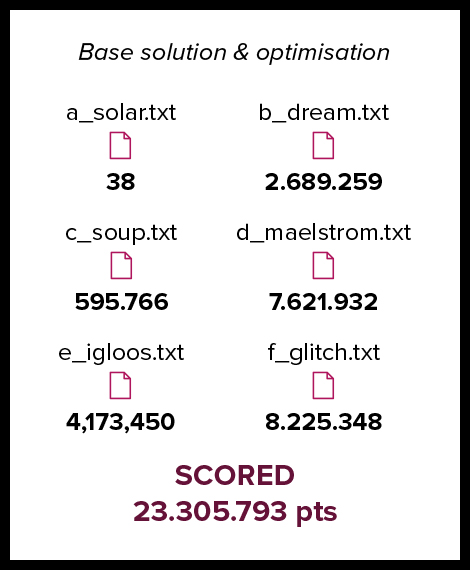
1. output a_solar.txt: 38 points (+2 points)
2. output b_dream.txt: 2,689,259 points (+19,379 points)
3. output c_soup.txt: 595,766 points (+4,996 points)
4. output d_maelstrom.txt: 7,621,932 points (+65,549 points)
5. output e_igloos.txt: 4,173,450 points (+197,400 points)
6. output f_glitch.txt: 8,225,348 points (+100,264 points)
Based on the final scores, with only the basic solution we’d have finished in 49th out of 2,862 teams in the official challenge.
The optimisation improvements may seems small, but remember in an optimisation problem every point matters. In fact, with an increase of just 1.69%, we climb the rankings from 49th to 34th place.



In this article we have shown that even the simpliest idea, if well implemented, can lead to great results even without any complex theoritical knowledge.
You can find the complete working source code here: solution.cpp. To run the solution it's enough a C++ compiler and, optionally, the OpenMP API if you want to parallelize the execution. The instruction on how to compile, run and test the solution are written in the comments.
In April 2020 we have done a live coding webinar of this solution and commented it with the Code Master team, you can see it here!
In the next articles we will analyze other previous challenges in order to prepare you for the Reply Code Challenge 2021!
Want to be the next winner?
Register on Reply Challenges and get updates on the next challenge!